숫자에, 쉽게, 속아 넘어가지 말아라!
(수학은 그냥 장식물이 아니란다!)

~ 이상봉 / 철학박사

1) 어떤 식당에 들어가서, 9” Pizza (9인치 피자)를 주문하였다.
2) 그런데, 식당의 종업원이 5” Pizza (5인치 피자) 2개를 가져와서,
“9인치 피자가 없어서, 그 대신에 5인치 피자를 2개 드립니다.
그러면, 손님께서는 같은 가격에
결국 1인치를 더 드시는 것이 되겠습니다!” 라고, 하였다.

자! 이럴 경우에…
그대! 그대는 어떻게 생각하는가?

과연? 종업원의 말대로 1인치를 더 먹게 되는 것일까?

그대!
그대도, 틀림없이, 원(圓)의 면적(面積)에 대해서 배웠을 것이다!

“원의 면적” 계산법:
원주율(파이) X 원의 반지름(r) X 원의 반지름(r).

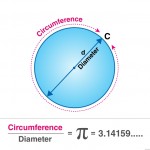
[원주율(파이, π ) = 3.141592.
(원의 둘레는, 직경의 3.141592배 라는 의미.)
π = C/ D,
C= circumference(원 주위), D= diameter(직경)
이것을, 파이(π, pi) 라고 한다. R = radius(반경)]

이 계산법에 의거하여…
9” 피자와 5” 피자의 면적을 계산하여 보자!

9” 피자의 면적은 3.141592 x 4.5 x 4.5 = 63.62 sq. Inch다.
5” 피자의 면적은 3.141592 x 2.5 x 2.5 = 19.63 sq, inch다.

그리하여…
5” 피자 2개면 19.63 x 2 = 39.26,
3개면 19.63 x 3 = 58.89,
4개면 19.6 3 x 4 = 78.52가 된다.

그러니까…
5” 피자 3개라도 9” 피자가 될 수 없다!
결국은, 5” 피자 4개가 되어야만 9” 피자 1개와 비슷한 셈이다.

따라서…
두 사람이 식당에 들어가서,
9” 짜리 대신에, 5” 짜리 두개 씩을 받아먹게 되면…
그 때에는, 아주 많은 가격의 손해를 보게 되는 것이란다!

자! 이래도…
수학 공부를 무시하고 또한 우습게 여기려고 하려는가?

——————————–

사족:
이미, 지나간, 부질없는 옛날 이야기일 뿐이지만…
내가 학교를 다닐 때의 수업이나 선생님에 대한 비난을
하고 싶은 마음은 전혀 없으나…
그래도, 한마디 하고 넘어가야만 되겠다.

나는, 사실상, 제대로 된 수업다운 수업을, 받아 본 적이 없는 것 같다.
그렇다 보니… 필요없는 고생을 많이 해야만 되었을 것이고…
그리하여, 억울하다!는 심정이 저 내부에
지워지지 않는 앙금으로 남아 있는 것 같다.

[하긴, 내가 다닌 학교의 교육만 그랬던 것도 아닐 것이고…
내가 받은 수업만 그랬던 것도 아닐 것이리라!
그 당시의 모든 수업들이 그렇듯이…
영어시간이 그랬고, 수학시간이 그랬고, 과학시간이 그랬고…
하다못해, 그 체육시간은 더욱 더 그렇고 그랬을 뿐이 아닌가?

그래서…
학교에 내는 돈만 아까운 것이 아니라…
학교를 오고 가고, 학교에서 보내는 시간 조차도 아까운 생각이 들었다!
(내가 학교를 다닐 때에는, 국민학교 조차도 무상교육이 아니었다.
수업료를 내야만 학교를 다닐 수 있었다.
수업료를 못내는 학생은 학교를 다닐 수 없었다.)}

그렇다!
수학 공식(公式)이나 계산법이,
어떻게 나오게 되었는지?에 대한 설명은 전혀 없이…
무조건적으로 공식이나 계산법만 외어서,
계산을 하도록 수업을 받았기 때문에…
나, 역시, 이 글의 본문에 나오고 있는 “원(圓)의 면적” 계산법이,
어떻게 해서 나오게 된 것인지도 전혀 모른 채…
단지, 그 公式만 외어서, 써먹어 왔을 뿐이다!

그런데…
이곳(미국)에 와서,
어쩌다가 그것에 대한 이야기가 나온 적이 있어서,
그 “원의 면적” 계산법이 어떻게? 나오게 되었는지?에 대하여,
아주 자세한 설명을 듣게 된 적이 있었는데…
그 때, 나는, 기쁨의 환호성이 터져 나왔다.

그러니…
만약에, 그대가,
아직도 원의 면적 계산법이,
어떻게? 나오게 된 것인지?를 모르고 있다면…
이제라도, 그 계산법이 어떻게 나오게 된 것인지?에 대하여,
확실하게 알게되면…
그대도, 또한, 커다란 기쁨을 느끼게 되지 않을까?

~Sang Bong Lee, Ph.D.,
Dr. Lee’s Closing Arguments,
Dr. Lee’s Lessons: Discovering Your Nature,
Dr. Lee’s Iconoclasm.
Dr. Lee’s an effable and ineffable.
All rights reserved and copyrighted.
(무단복제사용을 금함)